Fortune Tellers: Exploring Area
Submitted By:
Frequently in mathematics, students memorize and use formulas without understanding where they come from or why they work. In this lesson, students use paper fortune tellers to see how the areas of common polygons (triangles, trapezoids) can be found by decomposing and rearranging the shapes to make rectangles. They also explore the relationships between areas of the shapes that are made in the process of making their own fortune teller. Another version of this lesson, Fortune Tellers: Shapes and Area, in which students identify shapes and find areas by counting squares, is available for grades 3-4.
- A fortune teller made out of a square of white paper for class demonstration
- Scissors
Make a fortune teller beforehand, and start by asking about students’ prior knowledge:
- Has anyone seen one of these before? What do you know about it? (Note: Students may also call these “cootie catchers,” so be prepared to discuss respectful language and actions. Explain that you’ll be calling them “fortune tellers” for this lesson.)
- Has anyone ever made one? Do you know how to make one?
Show them the completed fortune teller and ask them to make some observations about it. Pose some questions that get them to think about the mathematics. Don't worry about coming to correct answers to these problems right now, the goal is just to get them to start thinking mathematically.
- What shapes do you see? (Geomerty)
- What the portion of the folded shape is made by each section? (Fractions)
- What is the chance of opening a specific panel? Are all panels equally probable? How do you know? (Probability)
Explain that today you’ll be exploring the shapes and their areas that result from making fortune tellers our of a square piece of paper.
The Fortune Teller Student Handout contains some facts about Origami that you can use to begin the discussion. If you have some students who are familiar with how to make Fortune Tellers and some who are not, pair them up accordingly.
Tell students that although they may already know how to make fortune tellers, right now they will be studying them as mathematicians. This means that they will be pausing after each step to make observations and calculate the area, not rushing to finish the fortune teller. Explain that you will do the first few steps together as a class, and then they will work independently or with a small group for the rest of the steps.
Start by giving students the 8x10 Grid for Making Fortune Teller.
- What is the area of this rectangle? How do you know? Encourage students to list several strategies for finding the area: counting all of the squares, counting by 8s, counting by 10s, multiplying 8 × 10 using known facts, etc.
- What do we mean when we talk about the area of a shape? Review that area is the amount of space a “flat” (2-dimensional) figure takes up.
- What are the units we use to measure area? Review that a square unit is a square with sides equal to the unit in length. It can also be written unit2. Some area measures may be made in square inches (1 inch × 1 inch) or square centimeters (1 cm × 1 cm).
- What is the general formula for the area of this shape? Discuss that the area of any rectangle can be found by multiplying the length by the width.
- The first step of making a fortune teller, like all Origami, is to start with a square. If I wanted to make a square, how would I have to change the shape? (Make all sides 8 units long).Have students cut out an 8x8 square from the grid.
- What is the area of the shape now? (64 sq units)
- What is the formula for the area of a square? Discuss that because the length and width are the same for squares, the area is the side length squared.
- Designate a section of the board for formulas (which you will add to throughout the lesson). Write the formulas using variables. (Rectangle: A = lw. Square: A = s2)
The Fortune Teller Student Handout has step-by-step instructions for making a fortune teller and finding areas. Demonstrate (or have a volunteer demonstrate) the first step of making the fortune teller, putting the grid paper face down and folding it corner to corner. Work with students to describe and find the area of the new shape:
- Ask: What shape is this and how do you know? (It is a right triangle, because one if its angles is 90°, and an isosceles triangle because two of its sides and two of its angles are congruent. Thus, it is a right isosceles triangle.)
- Give students several minutes to find the area and explain their methods. Some possibile strategies include: counting all the squares and combining the half squares to make whole squares, recognizing that the folded shape is 1/2 of the original square, adding together the area of several smaller rectangles within the triangle and combining half squares.
- If students do not recognize that the triangle has half the area of the square, or that two half-units can be put together to make a whole unit, guide them to make these observations.
- Introduce or review the terms base, height, and altitude here.
Key mathematical terms: area, square unit, formula, base, height, altitude
Students can work in pairs to complete the next steps of making a fortune teller on their own, following the instructions on the handout. After each step, students should identify the shape, its area, and its area relative to the original square. Have students justify each label or calculation, offer several methods, and support or correct each other to find the information. If students already know the formulas, they should find another way to prove the area and try to justify the formula.
To find the area of the trapezoid, suggest that students use some of the same strategies that they used for finding the area of the squares and triangles earlier. Possible strategies include:
- Counting squares and combining partial squares
- Moving triangle on one side over to the other side and flipping it upside down to make a 6 x 2 rectangle
- Flipping a small rectangle on each side up to create a 6x2 rectangle (which is the same result as counting squares and combining partial squares)
The goal of this lesson is for students to derive the formulas of squares, rectangles, and triangles, trapezoids using their relationship to rectangles. In the discussion, have students share their strategies and guide them to make connections to the formulas. In particular, you can develop connections to the formula for the area of a triangle and help students understand that any side of a triangle can be considered a base by discussing and comparing strategies for the triangles in Step 3 and Step 6.
- Ask students to share and justify their strategies for finding the area and then ask how does that relate that to the area of a square?
Triangle in Step 3: This triangle has an area of 8 square units. It is easy to measure the base and height as the sides of the right angle (the legs). When the flap is unfolded, it is easy to see that these are also the sides of a 4 x4 square and the triangle has half the area of the square. In other words, the square is composed of two right triangles.
Triangle in Step 6: This triangle is oriented differently on the grid paper so that you can see the hypotenuse as the base of 4 and the altitude as 2. When folded in you can also see that it's area is half of a 2 x 4 rectangle, as shown below.

Trapezoid (between Step 6 and 7)
- Have students share and justify their strategies for finding the area of the trapezoid. Make sure students see how the trapezoid can also be decomposed into a rectangle and two triangles and how it can fit inside a 8x2 rectangle.
- The Trapezoid Challenge described in extensions below can be used to show the connection to the formula for finding the area of a trapezoid. For now, focus on decomposition and the relationships to rectangles to justify area.
Decomposition refers to finding the area of a shape by breaking it into smaller pieces whose areas can be calculated more easily, then adding those areas together.)
- Have students look at the seemingly-irregular shape on the handout. How could you use some of the strategies from today to find the area of a shape like this?
Have students create fortune tellers to practice remembering the formulas or geometric definitions by writing a shape on the outside and the formula or definition on the inside.
Triangle Challenge
Review the first triangle from Step 1 of the Fortune teller that had a base of 8 and an altitude of 8. Use the attached Triangle Challenge to challenge students to create different triangles with a base of 8 and an altitude (height) of 8 on the grid paper. (Note: the triangle will have different angles)
- Give students several minutes to find the area of the new triangle and explain how they found it.
- Have students share the area of each of their triangles. Guide students to notice that even though they placed their altitudes in different locations, they all have the same area of 32 square units. Discuss that the area of the triangle is based on the base and the height, not how close the altitude is to one side or another.
- Record the methods students used to find the area on the board. Some possible methods are listed in the Possible Student Solutions.
- Insure that the class understands that the area of the triangle is half of the area of the square using your own 8 × 8 square. Draw your own triangle with a base of 8 and a height of 8, then cut it out. Rotate the two triangular pieces that are left over to cover the original triangle, demonstrating that they have the same area.
- As a class, come to the consensus that the area of a triangle is always half of the area of the rectangle (or square) that is defined by its base and height.
- Discuss how to write this as an equation with variables. Record the new formula A = ½bh.
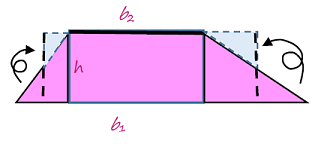
Parallelogram Challenge
Use the attached Parallelogram Challenge to help students derive and justify the formula for finding the area of a parallelogram. Students should notice that the triangle on one side of the parallelogram can be cut off and moved to the other side to make a rectangle with the same base and height as the original paralleogram. Thus, the formula is A = bh.
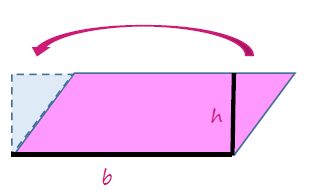
Trapezoid Challenge
Use the attached Trapezoid Challenge to help students derive and justify the formula for finding the area of a trapezoid. Students should notice that if the triangle on each end is cut vertically in half and then the bottom half is moved up to the top, it creates a new rectangle. This new rectangle has the same height as the original trapezoid. Its new base is the average of the two original bases, or (b1 + b2) / 2. Thus, the area of a trapezoid is A = ½(b1 + b2)h.
Read more about math and origami:
- http://www.langorigami.com/
- http://mathigon.org/mathigon_org/origami/
- http://www.paperfolding.com/math/
Have students learn to make other origami structures and determine the area of each shape for the major folds using the formulas derived in this lesson, decomposition, and counting squares (for confirmation).

 8x10 Grid for Making Fortune Teller
8x10 Grid for Making Fortune Teller





Comments
(no comments)