How Much Battery?
Submitted By:
In this one-day lesson, students use their knowledge of fractions to estimate how long it takes phone batteries to charge. This is a rate problem, and also an opportunity for students to deepen their understanding of fractions and percents, using a context they are familiar with and a visual bar model. Students use their implicit knowledge of phone battery to estimate how much battery is left using percentages or fractions, and then develop their own strategies to estimate how long the battery will take to charge.
Tell students that today they’re going to exploring the time it takes to charge a phone battery. Ask students if they have ever found their phone battery low and needed to charge it quickly. (You might tell students a story about your own phone battery).
Show students the following picture of a phone battery. Ask students how long they think it’ll take you to get to full charge? Ask them to explain their reasoning behind their estimates.

Use this context and the visual model to reinforce the idea that 12% means 12/100—if we cut the battery up into 100 equal pieces, and shade 12 of them, this would represent 12%.
Tell students that you’ve been doing some research on phone battery, and you’ve found the following (display this for students):
This iPhone can charge 50% of its battery in 30 minutes. How long will it take to charge fully?
Work with students to make sense of this question. Reinforce the idea that this is 50/100, or 1/2. You might draw the following image on the board, to help scaffold understanding:
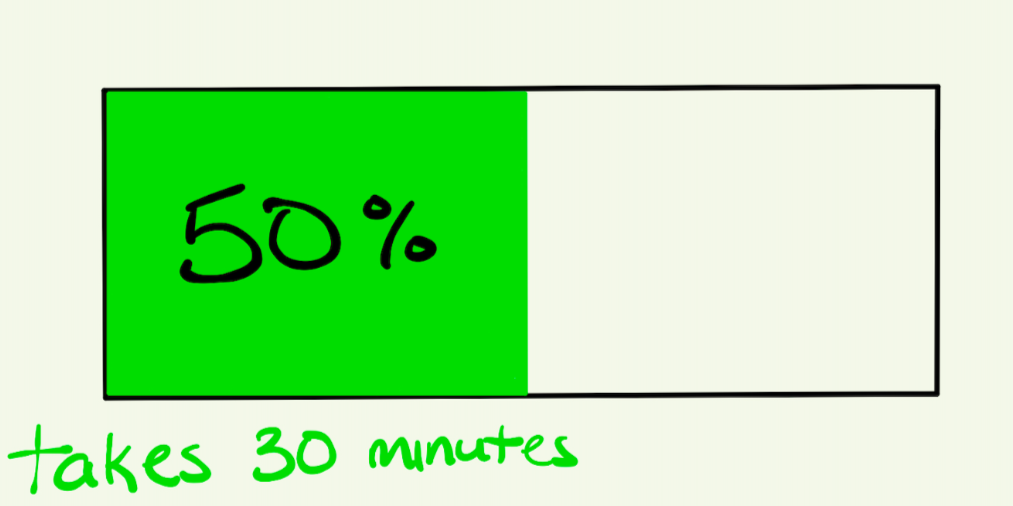
Students should be able to double 30 minutes to arrive at 60 minutes or one hour.
Next pose the following question:
- What if your battery is 75% full. How long will it take to charge to full?
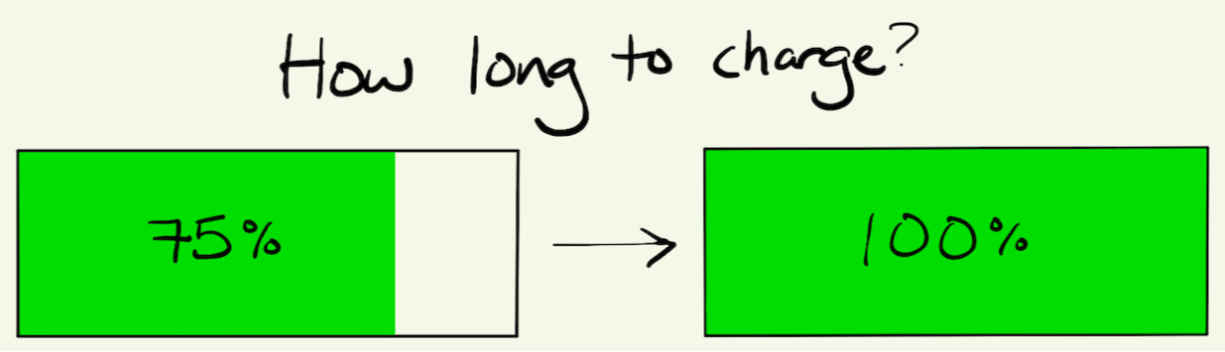
After giving students some quiet think time, have them share their answers and strategies. Students will likely reason along the following lines: the battery needs to charge another 25%; because 25% is half of 50%, it will take half the time to charge, i.e. 15 minutes. While discussing strategies, encourage the class to convert between fractions and percents. Using language like “a half,” as in “25% is half of 50%” can help reinforce this. If students don’t naturally convert these percentages to fractions, you can use fraction language when revoicing their strategies. As in: “So you already knew half the battery took 30 minutes to charge, and you knew that we had one fourth of the battery we needed to charge.” Pictures can help reinforce this conversion. The image below highlights unit fraction reasoining by showing that the whole is made up of four 1/4's (1/4 + 1/4 + 1/4 + 1/4) and that 1/2 is equivalent to 1/4 + 1/4 or 2/4.
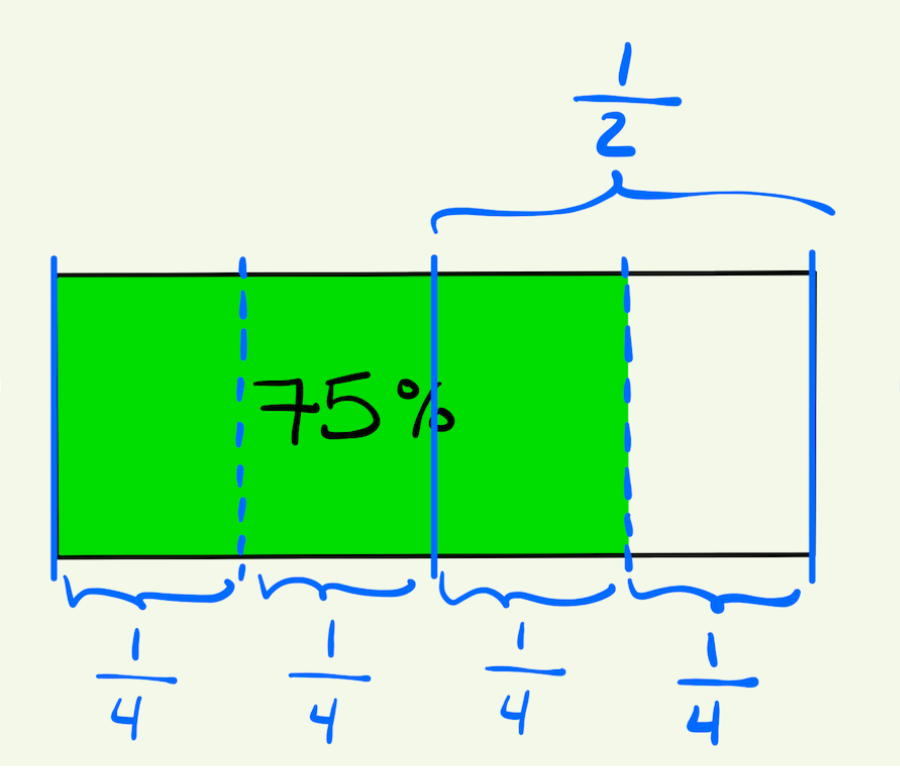
To give students more practice thinking about this, you can give them another problem: How long would it take to fully charge your battery if you started at 25%? Work in a similar way with this problem to help students visualize how to break the battery into fractional parts. Fractions are a useful way of thinking about this problem, and the visual of the battery provides a helpful model.
Hand out the “battery picture” to students, so that each student has a copy that they can draw on/cut out/fold/etc.
Introduce the main task that students will be working on:
- The “battery picture” shows that your battery at 12%. Your job is to estimate how long it will take to charge the battery to 100%.
Clarify that they don’t need to get an exact answer. You’re more curious to see how they go about finding as exact an answer as possible.
Before releasing students to exploration, make sure they have a way to start thinking about the problem, but don't give them a strategy to use.
Have students work in small groups to estimate how long it’ll take the battery to charge. For groups who are stuck, you can ask probing questions. For example:
- How could we figure out how much of the battery we need to charge?
- In the example problems, we broke the battery in half, and then into quarters. How might we break the battery into pieces in this case to better understand it?
- Does the amount of battery remaining look close to any familiar fractions? Or, what ways could we use to estimate how much of the battery is left as a fraction?
For groups who finish early, challenge them to come up with a more exact estimate. Or have them work in small groups on the worksheet in the resources section, which gives various other problems that will challenge them to estimate fractions by sight, convert between fractions and percentages, and use unit fraction and unit rate reasoning to solve problems.
Bring students back together to share their strategies, both from the original problem and from select problems on the worksheet. See the resources section for different possible approaches students might take. Compare and contrast solution strategies so that students can see different methods of solving the problem. Highlight solutions that feature fraction/percent conversion, double number lines, unit fraction reasoning, and unit rate reasoning. Remember to include visual models!

 Battery Picture
Battery Picture


Comments
(no comments)